Маленькие трагедии в классической физике
Валентин Федоров, Дмитрий Пономарев
ноябрь 2001 года
Содержание
Пример 1. Движение в центральном поле.
Пример 2. Кеплерова задача
Пример 3. О сферических координатах.
Пример 4. Об экспериментальной проверке
рожденного "на небесах" закона всемирного тяготения Ньютона в Земных
условиях (опыт Кэвендиша).
Пример 1. Движение в центральном поле
(Л.Д.Ландау, Е.М.Лифшиц, Теоретическая физика, т. 1. Механика,
М., "Наука", 1988, стр. 46 - 47).
"В данном случае обобщенный импульс
![]()
совпадает с
моментом Mz = M (см.
(9,6)), так что мы возвращаемся к известному уже нам закону сохранения момента
![]() .
...............................................(14,2)
.
...............................................(14,2)
.... Полное
решение задачи о движении частицы в центральном поле проще всего получить,
исходя из законов сохранения энергии и момента, не выписывая при этом самих
уравнений движения. Выражая ![]() через М
из (14,2) и подставляя в выражение для энергии,
получим:
через М
из (14,2) и подставляя в выражение для энергии,
получим:
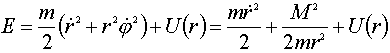 .
...................(14,4)
.
...................(14,4)
Отсюда
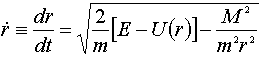 .......................................(14,5)
.......................................(14,5)
или, разделяя переменные и интегрируя:
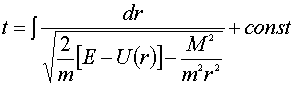 . ................................(14,6)
. ................................(14,6)
Далее, написав (14,2) в виде
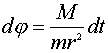 ,
,
подставив сюда dt из (14,5) и интегрируя, находим:
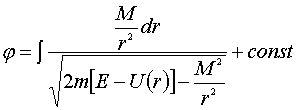 . .........................(14,7)
. .........................(14,7)
Формулы (14,6) и
(14,7) решают в общем виде поставленную задачу. Вторая из них определяет связь
между r
и ![]() , т.е. уравнение траектории. Формула же (14,6) определяет
в неявном виде расстояние r движущейся точки от центра как функцию времени. ......."
, т.е. уравнение траектории. Формула же (14,6) определяет
в неявном виде расстояние r движущейся точки от центра как функцию времени. ......."
Выводы поразительны по своей
необоснованности, так как:
а) Учитывая (14,5), выражение (14,6) есть не
что иное, как
![]() ,
,
а это значит, что (14,6) только в НЕЯСНОМ (здесь опечатки нет!) для учащихся всех уровней виде определяет расстояние r движущейся точки от центра как функцию от времени;
б) Поскольку
числитель подинтегрального выражения есть ![]() , а
знаменатель
, а
знаменатель ![]() , то выражение (14,7) должно записываться только так:
, то выражение (14,7) должно записываться только так:
![]() .
.
В этом случае
усмотреть связь между r и ![]() может
только сумасшедший. Пустая игра в математические формулы еще никогда к
полезному результату не приводила.
может
только сумасшедший. Пустая игра в математические формулы еще никогда к
полезному результату не приводила.
Пример 2. Кеплерова задача (см. там же, стр.51 -
52).
"Важнейшим
случаем центральных полей являются поля, в которых потенциальная энергия
обратно пропорциональна r и соответственно силы обратно пропорциональны r². Сюда
относятся ньютоновские поля тяготения и кулоновские
электростатические поля; первые, как известно, имеют характер притяжения, а
вторые могут быть как полями притяжения, так и отталкивания.
Рассмотрим сначала поле притяжения, в котором
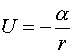 .........................................................(15,1)
.........................................................(15,1)
с положительной постоянной ![]() . ....
. ....
Форма траектории
получается с помощью формулы (14,7). Подставляя в нее ![]() и
производя элементарное интегрирование, получим:
и
производя элементарное интегрирование, получим:
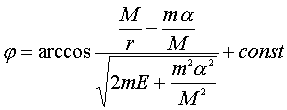 .
.
Выбирая начало отсчета угла ![]() так,
чтобы const=0,
и вводя обозначения
так,
чтобы const=0,
и вводя обозначения
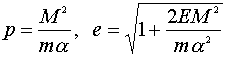 ,
.......................................(15,4)
,
.......................................(15,4)
перепишем формулу для траектории в виде
![]() .
...................................................(15,5)
.
...................................................(15,5)
Это есть уравнение
конического сечения с фокусом в начале координат; p и e - так называемые параметр и эксцентриситет орбиты. ......"
Уникальный
результат, явно противоречащий уточненному в предыдущем примере виду и смыслу
выражения (14,7), но ярко демонстрирующий околоматематический
способ обоснования канонизированных законов Кеплера (первый - каждая планета
движется по эллипсу, в одном из фокусов которого находится Солнце; второй -
секторная скорость каждой планеты относительно Солнца постоянна).
Поскольку
канонизированные законы составляют фундамент теоретической физики, то право на
отрицание любого из них появляется лишь тогда, когда обнаруживается ХОТЯ БЫ ОДНА принципиальная ошибка в его математическом
обосновании.
Таковые в
рассматриваемом примере есть, но они скрываются за элементарным интегрированием
неизвестного выражения, которое при наличии результата (15,5) путем обратных
математических операций легко отыскать и подвергнуть при необходимости анализу.
Выражение (15,5)
есть уравнение кривой второго порядка в полярных координатах, где фокус принят
за полюс, а ось симметрии за полярную ось. Из этого следует, что полярный
радиус-вектор любой точки кривой (15,5) записывается в виде
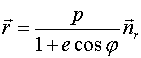 ,
,
где p и e - параметр и эксцентриситет орбиты, ![]() - орт
полярных (цилиндрических) координат, а значит
- орт
полярных (цилиндрических) координат, а значит
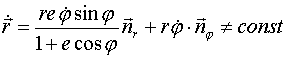
и, следовательно
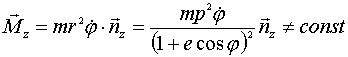
(радиус-вектор
точки, ее скорость движения и момент при ![]() являются
функциями времени).
являются
функциями времени).
В связи с тем, что
"форма траектории получается с помощью формулы (14,7)" (забудем на
мгновение о ее математическом смысле), которая получена "из законов
сохранения энергии и момента" (пример 1), то налицо вопиющее противоречие
- момент при движении точки по эллипсу не является величиной постоянной. Такое
противоречие снимается, если эксцентриситет орбиты равен нулю, а это уже
окружность и движение осуществляется с постоянной угловой скоростью, но это уже
не законы Кеплера.
Вот так математически обоснованы два закона Кеплера, а ведь они
относятся к перечню фундаментальных теоретической физики!
Пример 3. О сферических координатах.
Предметом внимания
будет обсуждение вопроса о правомерности записи выражений
проекций ускорения движущейся точки в сферических координатах, когда не
только величина радиус-вектора точки, но и два угла задаются некоторыми функциями
единого параметра t,
именуемого временем, то есть ![]() .
.
Рассмотрим случай, когда разложение радиус-вектора точки по ортам сферических координат и сами орты определяются формулами (см., например, И.И.Ольховский Курс теоретической механики для физиков. М., Изд-во Моск. ун-та, 1978, стр. 17, 228)
![]() ,
..........................................................................(1)
,
..........................................................................(1)
![]() , ....................................(2)
, ....................................(2)
![]() , ...................................(3)
, ...................................(3)
![]() .
...................................................(4)
.
...................................................(4)
Принимая во
внимание, что направления ортов ![]() зависят от положения точки (времени), для ее скорости
записывают выражение
зависят от положения точки (времени), для ее скорости
записывают выражение
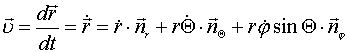 , ....................................(5)
, ....................................(5)
а для ускорения
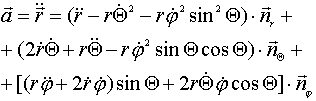 . .....................................(6)
. .....................................(6)
Если траектория
движения точки задана в виде (1), а орты сферических координат определены
выражениями (2) - (4), где ![]() являются функциями единого параметра t (одного из
самых загадочных в теоретическом ЕСТЕСТВОЗНАНИИ), то есть все основания
считать, что выражение (6) принципиально ошибочно. Об этом свидетельствует даже
сам вид функциональной зависимости проекции ускорения на направление
являются функциями единого параметра t (одного из
самых загадочных в теоретическом ЕСТЕСТВОЗНАНИИ), то есть все основания
считать, что выражение (6) принципиально ошибочно. Об этом свидетельствует даже
сам вид функциональной зависимости проекции ускорения на направление ![]() от
от ![]() , чего
быть не должно. Двукратное дифференцирование
синуса или косинуса не приводит к квадрату этих тригонометрических функций,
а поэтому путем непосредственного дифференцирования выражения (1) с учетом (2),
считая
, чего
быть не должно. Двукратное дифференцирование
синуса или косинуса не приводит к квадрату этих тригонометрических функций,
а поэтому путем непосредственного дифференцирования выражения (1) с учетом (2),
считая ![]() функциями параметра t, подтвердим
это заключение.
функциями параметра t, подтвердим
это заключение.
Дифференцируя дважды по t выражение
![]() .........................(7)
.........................(7)
получим
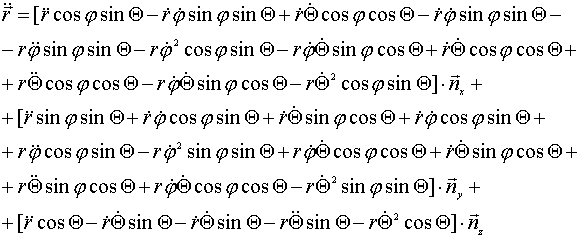 . .....(8)
. .....(8)
Используя обозначения (2) - (4), последнее
запишем в таких вариантах:
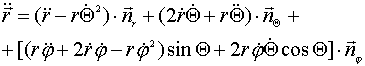 ............................(9)
............................(9)
и
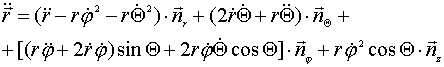 . .................(10)
. .................(10)
Полученный
непосредственным дифференцированием результат явно не согласуется с (6), а
поэтому общепринятый обходной способ получения
проекций ускорения в сферических координатах, мягко говоря
и даже очень, ошибочен.
Но и
это еще не все, так как противоречия здесь куда более значимы, чем указанное.
Напомним
(А.Ф.Бермант, И.Г.Араманович
Краткий курс математического анализа для втузов. М., "Наука", 1971, стр.
142): Задание функциональной зависимости между двумя переменными,
состоящее в том, что обе переменные определяются каждая в отдельности как
функции одной и той же вспомогательной переменной, называется параметрическим,
а вспомогательная переменная - параметром.
Отыскание по системе
![]() ............................................................(11)
............................................................(11)
непосредственной
связи между переменными x и y без участия
вспомогательной переменной t называется исключением параметра. В результате
исключения параметра получаем уравнение между x и y, задающее одну из
этих переменных как явную или неявную функцию другой. Если x и y независимые переменные, то говорить о существовании
параметра для этих переменных бессмысленно.
Гипотеза
о зависимости ![]() от единого параметра t не имеет права на свое существование, поскольку она лишена всякого
смысла.
от единого параметра t не имеет права на свое существование, поскольку она лишена всякого
смысла.
Действительно, если
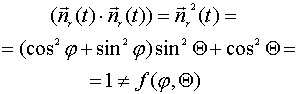 ....................................(12)
....................................(12)
определяет
сферическую поверхность единичного радиуса (Внимание,
СФЕРИЧЕСКУЮ ПОВЕРХНОСТЬ, А НЕ КРИВУЮ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ!), то
под выражением (2) необходимо понимать только параметрическую кривую,
принадлежащую сфере единичного радиуса, а поскольку параметрами задания кривой ![]() на сфере единичного радиуса являются
на сфере единичного радиуса являются ![]() , то гипотезировать о
зависимости их от единого параметра бессмысленно (см., например, Г.Корн и
Т.Корн Справочник по математике для научных работников и инженеров. М., "Наука",
1973, стр. 78).
, то гипотезировать о
зависимости их от единого параметра бессмысленно (см., например, Г.Корн и
Т.Корн Справочник по математике для научных работников и инженеров. М., "Наука",
1973, стр. 78).
Под выражением
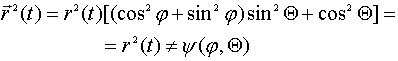 .......................(13)
.......................(13)
необходимо
понимать семейство концентрических сфер, которые никогда не пересекаются друг с
другом, а поэтому лишено здравого смысла выдавать
дискретно изменяющиеся радиусы концентрических сфер за непрерывно изменяющуюся
величину. (Здесь возникают непреодолимые трудности для использования аппарата
дифференциального исчисления.)
Из отмеченного
следует, что под выражением
![]() .........................................................(14)
.........................................................(14)
необходимо
понимать двухпараметрическую кривую, принадлежащую только конкретной сфере
радиуса ![]() .
.
Не
следует повторять в общем-то аналогичных доказательств
для цилиндрических координат, а сразу отметим, что гипотеза о зависимости ![]() от единого параметра t, именуемого в теоретическом естествознании временем, также ошибочна.
от единого параметра t, именуемого в теоретическом естествознании временем, также ошибочна.
Пример 4. Об экспериментальной проверке рожденного
"на небесах" закона всемирного тяготения Ньютона в Земных условиях
(опыт Кэвендиша).
Сегодня обыденно
звучит и воспринимается утверждение о том, что закон всемирного тяготения
Ньютона является экспериментально подтвержденным законом природы, а не каким-то
полуматематически обоснованным и полуфизически
осмысленным умозаключением Ньютона, сделанным на основании астрономических
наблюдений. Такое утверждение базируется на эксперименте Генри Кэвендиша (1798 г.), которому якобы удалось проверить его
соблюдение на притяжении тел не к нашей планете, а между собой.
Безусловно, сама
идея проверить закон, рожденный "на небесах", в Земных условиях
великолепна, но требует вполне конкретной теоретической обоснованности
методики эксперимента, которой только и имеет смысл руководствоваться при
осуществлении эксперимента. Если методическая часть является теоретически не
подготовленной, то эксперимент будет не целенаправленным и не решит
поставленной задачи, а результаты измерений станут холостым выстрелом по
воробьям - шума много, а трофеев нет.
Закон одномерного
движения для двух гравитационно взаимодействующих тел
в отсутствии других внешних воздействий запишем в виде
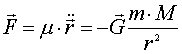 ,
......................................................(1)
,
......................................................(1)
где
![]() - сила гравитационного взаимодействия между телами,
m, M -
масса тел соответственно,
- сила гравитационного взаимодействия между телами,
m, M -
масса тел соответственно, 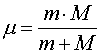 - приведенная масса, r - расстояние между центрами масс тел,
- приведенная масса, r - расстояние между центрами масс тел, ![]() - универсальная гравитационная постоянная,
- универсальная гравитационная постоянная, ![]() - ускорение сближения тел (см., например,
И.И.Ольховский Курс теоретической механики для физиков. М., Изд-во Моск.
ун-та, 1978, стр. 116).
- ускорение сближения тел (см., например,
И.И.Ольховский Курс теоретической механики для физиков. М., Изд-во Моск.
ун-та, 1978, стр. 116).
Выполняя элементарные преобразования, закон движения запишем в виде
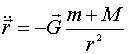 ,
................................................................(2)
,
................................................................(2)
который и является базисным теории гравитации Ньютона в
дифференциальной форме.
Поскольку
универсальная гравитационная постоянная ![]() есть векторная размерная величина
есть векторная размерная величина ![]() , то
не составляет особого труда по размерности восстановить ее истинное содержание:
, то
не составляет особого труда по размерности восстановить ее истинное содержание:
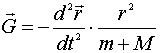 . ............................................................(3)
. ............................................................(3)
Используя (3), уточним смысл закона
всемирного тяготения:
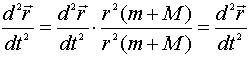 .
..................................................(4)
.
..................................................(4)
Результат в виде
(4) должен восприниматься как закономерный и другого ожидать не следовало,
поскольку во всем теоретическом естествознании, начиная от Ньютона и до наших
дней, понятию времени отводилась и отводится наравне с понятием массы, заряда,
расстояния (пространства) самостоятельная роль - роль базисного понятия. (Базисные понятия - первичные сущности любой теории и не
могут истолковываться посредством других базисных понятий этой же теории!)
Смысл
записи закона всемирного тяготения заключается в задании некоторого физического
параметра t (времени) гравитационной системы двух тел
в виде функции базисных понятий указанной теории (массы и расстояния), т.е.
![]() ,
..............................................................(5)
,
..............................................................(5)
причем
такого параметра системы, с помощью которого непротиворечивым образом
описываются как одномерное движение тел, так и устойчивое движение тел разной
массы по концентрическим окружностям в противофазе.
Предположим, что
универсальная гравитационная постоянная является векторным подгоночным
коэффициентом в уравнении движения (2), тогда это дифференциальное уравнение
при постоянных G
и m +
M будет
уравнением с разделяющимися переменными. Разрешая его, находим
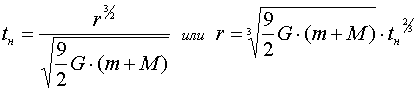 . ..........................(6)
. ..........................(6)
Результат по зависимости t = t(r) совпадает с третьим законом Кеплера (отношение квадратов периодов обращения планет к кубам больших полуосей их эллиптических орбит постоянно и для всех планет одинаково), но за таким результатом скрывается нечто, именуемое отрицанием устойчивого движения по окружности:
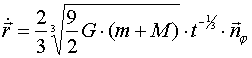 ...............................................(7)
...............................................(7)
и
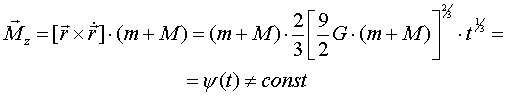 . .............(8)
. .............(8)
То,
что универсальная гравитационная постоянная является
подгоночным коэффициентом, сомнений не вызывает, поскольку ее значение
определяется из выражения
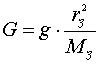 ,
....................................................................(9)
,
....................................................................(9)
где g - ускорение свободного падения тел (m << MЗ) у поверхности Земли, rЗ
- радиус Земли, MЗ
- масса Земли, а не какой-то другой планеты или
звезды.
Уточнение, в
первую очередь, массы Земли потребует изменения значения этой ВСЕМИРНОЙ
ФУНДАМЕНТАЛЬНОЙ ПОСТОЯННОЙ. (Такое должно быть исключено!)
На
основании изложенного приходим к однозначному выводу, что закон всемирного
тяготения Ньютона ОШИБОЧЕН, хотя Лаплас и назвал его "ВЕЛИКИМ ЗАКОНОМ
ПРИРОДЫ" (см. П.С.Лаплас Изложение системы мира. Л., "Наука", 1982, стр.
140) и считал, что все или почти все физические законы должны с некоторыми
видоизменениями повторять формулу записи закона Ньютона. Последнее воспринималось в те времена, да и в последующие, как
указание к действию, а подтверждением этому является наличие в современном
теоретическом естествознании нескольких размерных "ФУНДАМЕНТАЛЬНЫХ ФИЗИЧЕСКИХ
ПОСТОЯННЫХ".
Закон всемирного тяготения (теория
гравитации) записывается в виде
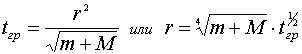 ,
..........................................(10)
,
..........................................(10)
где tгр - гравитационное время системы двух тел с массами m и M, а r - расстояние между центрами их масс. Величина скорости сближения тел (одномерное движение) и величина ускорения сближения тел определяются выражениями
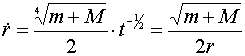 ................................................(11)
................................................(11)
и
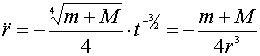 , ...........................................(12)
, ...........................................(12)
а движение тел ![]() по
концентрическим окружностям осуществляется в противофазе со строго
фиксированной ориентацией в пространстве. Центр концентрических окружностей
определяется из равенства моментов инерции этих тел.
по
концентрическим окружностям осуществляется в противофазе со строго
фиксированной ориентацией в пространстве. Центр концентрических окружностей
определяется из равенства моментов инерции этих тел.
Если
m << M,
то из этого следует, что величина ускорения
свободного падения тел g, например, у
поверхности Земли, определенная с использованием маятниковых часов, равна средней
плотности земных пород ![]() , умноженной на
, умноженной на ![]() , т.е.
, т.е.
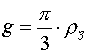 .
..............................................................(13)
.
..............................................................(13)
Соотношение (13)
впервые теоретически обоснованным способом позволяет определить среднюю
плотность пород нашей планеты и ее массу:
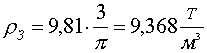 , .............................................(14)
, .............................................(14)
![]() . ..............(15)
. ..............(15)
Величина массы
Земли ![]() существенно отличается от общепризнанного значения
существенно отличается от общепризнанного значения ![]() и
объясняется это тем, что впервые исключено произвольное варьирование величин
G и
m + M
в выражении
и
объясняется это тем, что впервые исключено произвольное варьирование величин
G и
m + M
в выражении
![]() . .............................................(16)
. .............................................(16)
Полученное
теоретически обоснованным методом значение средней плотности земных пород коренным
образом изменяет современные взгляды на элементный состав и строение Земли.
Земля - сложный физико-химический объект Солнечной системы, внутри которого
активно идут не только геохимические и геофизические процессы, но и геоядерные. Последние идут более
активно, чем считают сегодня.
Безусловно, идея Кэвендиша фантастическая, но подтвердить принципиально
ошибочный закон тщательно спланированным и безукоризненно выполненным
экспериментом еще никому не удавалось.
Техническое
исполнение опыта (не серии
экспериментов с шарами из разного по плотности материала!) Кэвендиша
таково: Крутильные весы простейшей конструкции, состоящие из вертикальной
кварцевой нити, на которой подвешивался легкий уравновешивающий рычаг с
маленькими шариками на концах и два больших свинцовых шара диаметром примерно
по одному дециметру (плотность свинца 11,344 г/см³).
Суть опыта на языке математики с
использованием выражения (12):
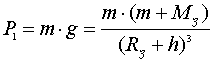 , .............................................(17)
, .............................................(17)
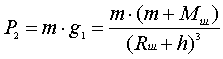 , .............................................(18)
, .............................................(18)
где P1 и P2 - вес пробного
тела в соответствующих гравитационных системах (шарик - Земля, шарик -
свинцовый шар), g
и g1
- ускорение свободного падения в соответствующих
гравитационных системах, m, MЗ и Mш
- масса шарика, Земли и свинцового шара
соответственно, r,
RЗ
и Rш -
радиус шарика, Земли и свинцового шара соответственно.
Разделим (17) на (18) и получим
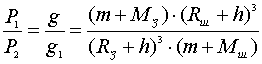 , ......................................(19)
, ......................................(19)
или в пределе ( m<<Mш )
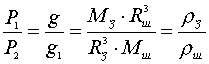 , ............................................(20)
, ............................................(20)
а это известно теперь и без опыта Кэвендиша.
вернуть к: Основы физики
Свои комментарии Вы
можете отправить:
info@timeam.ru
© В.В. Фёдоров, Д.А. Пономарёв. 1999-2018.
Сведения об
авторских правах.
Последняя проверка: 25 июня 2018.